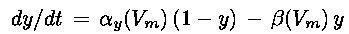The Hodgkin-Huxley Model Equations

In the 1950's Hodgkin and Huxley (1952) introduced the first continuum mathematical model designed to reproduce action potentials. Their model assumed that when the membrane potential was not equal to the equilibrium potential, there would be a net flow of ions proportional to the difference between the membrane potential and the equilibrium potential. Thus for an ion species labeled y with a corresponding current i_y, Ohm's law gave the equation i_y = (V_m - V_y)/r_y = g(V_m - V_y), where V_y is the equilibrium potential and r_y is the resistance to the flow of ions, which can be expressed in terms of a membrane conductance g_y.

The ionic conductance is, in general, a nonlinear function of the membrane voltage and can be represented by several channels. In cells, the ion channels are either open or closed, and in the case of voltage gating, the percentage of channels that are open out of the total number of channels in the cell is a function of the membrane voltage. Therefore, the probability function y (known as a gate variable) can be constructed to define what fraction of the channels are open as a function of voltage and time. Since gate variables range between 0 (all ion channels closed) and 1 (all ion channels open), the total cell or tissue conductance gion due to a given ion is given by g_ion = g y(t,V_m), where g is the maximum possible conductance obtained when all channels are open.

Hodgkin and Huxley found that squid axon sodium and potassium conductances, obtained from voltage-clamp techniques, could be reproduced by using gate variables obeying simple first-order equations of the form

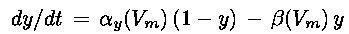(Eq. 1)

where 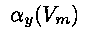and 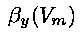can be complex functions of the voltage. These equations describe how the gates open and close at different time rates and as a function of voltage, thereby controlling the kinetics of ionic flow through the channels.

Hodgkin and Huxley reproduced the squid nerve action potential by using three different currents: a potassium current I_K, a sodium current I_Na, and a leak current later identified as chloride I_Cl. These three currents, whose sum is used to define the total ion current, are formulated as follows:

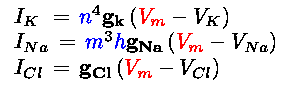(Eq. 2)

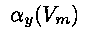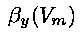where h, m, and n are the gate variables and V_m is the membrane voltage. The opening and closing of the potassium ion channels is given by the activation gate n , while the sodium channels are goverened by the activation gate m and the inactivation gate h . In this model the sodium activation gate m operates on a time scale several orders of magnitude faster than other gates. The functions and in this model take the following form:

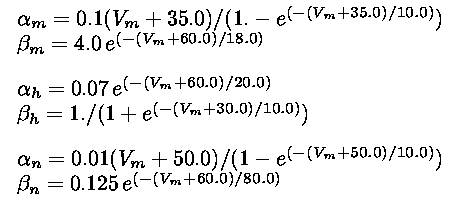
For further information about the model we refer to the original article: Hodgkin AL, Huxley AF. (1952) J Physiol 117, 500-540.

Back to the HH applet .