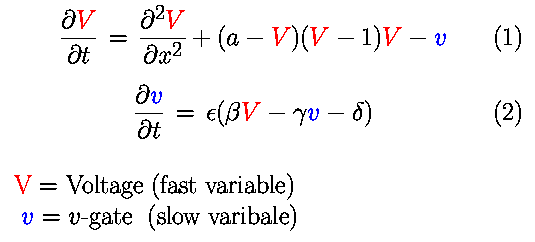FitzHugh-Nagumo (FHN) Model
for one cell
This applet shows the membrane potential produced by a cell
using the FHN model as a
function of time after it is stimulated above its threshold for excitation.
To use the applet, click the Start button to initiate
the simulation and the Reset button to return
the parameters to their initial values.
The FitzHugh-Nagumo model (FitzHugh, 1961) is a
generic model for excitable media and can be applied
to a variety of systems.
FitzHugh called his simplified model the Bon Hoeffer-van der Pol
model and derived it in the 1960s as a simplification
of the Hodgkin-Huxley equations.
The model adiabatically eliminates the h and m gates and
retains only a slow variable similar to n, denoted here as v.
Because of its simple two-variable form and generality,
it has been used widely.
The model is able to reproduce many qualitative characteristics
of electrical impulses along nerve and cardiac fibers,
such as the existence of an excitation threshold,
relative and absolute refractory periods,
and the generation of pulse trains under the action of external currents.
The model is implemented as described by the following equations:
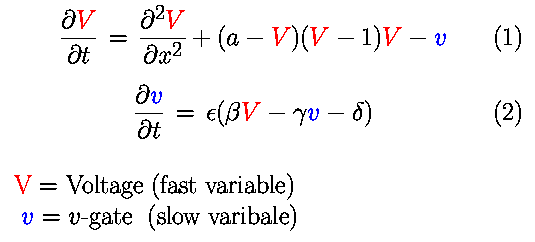
In the model, a represents the threshold for excitation;
epsilon represents the excitability; and beta, gamma, and delta
are parameters that can change the rest state and dynamics.
Since this is a generic model, time is represented
in dimensionless units for simplicity.
As in the Hodgkin-Huxley model applet, the FHN applet shows the activation produced by two external stimuli.
Increasing a from its initial value of 0.1 makes it more difficult for the external stimulus to produce an excitation until
at a =0.5, no activation is produced.
The reason is that the applet uses 0.5 as the magnitude
of the external stimulus.
If a instead is decreased to a value such as -0.1,
the resting potential becomes unstable. Under these conditions, the system will remain
at the resting potential if not perturbed, as can be seen by setting S1 and S2 to times larger than the integration time. However,
if an external stimulus is applied by setting S1 to 1, the system will exhibit auto-oscillatory behavior, similar to that seen in the
Hodgkin-Huxley model for large values of gNa.
The parameter epsilon is responsible for the different
time scales between the u and v processes and is sometimes
referred to as
the abruptness of excitation or excitability.
In the model, the smaller the value of epsilon,
the faster the action potential rate of rise and the longer
the action potential plateau.
Because the rate of rise is directly related to the
excitability of the system, in this model
decreasing epsilon increases the excitability and the
action potential duration.
These effects can be observed in the applet by setting
both S1 and S2 to 1 and by varying epsilon from 0.01 to 0.0001 and
increasing the integration time as needed to see the full activation.
The FHN applet also can demonstrate how the interval of time
between two action potentials can affect the second action potential.
For instance, set epsilon to 0.0001, S1 to 0, and
integration time to 700. Then alter the timing of S2.
Notice that a second activation
is not produced for S2 below the value 464.
When S2 = 464, an activation finally becomes possible, but the duration of the
activation is less than half that of the previous activation. By increasing time to 2000 and by continuing to increase S2,
it can be seen that S2 must be at least 1500 in order for the system to recover its original properties and to produce a second
action potential as long as the first. The relationship between the duration of an action potential (APD) and the amount of time between the
previous activation and the second stimulus (diastolic interval or DI) is known as restitution and is an important characteristic
of cardiac tissue. When the heart rate increases, such as during exercise, the lengths of cellular signals that initiate muscular
contractions are shortened in a similar way to ensure that filling of the heart chambers and ejection of blood occur efficiently.
Without such adaptation, the ventricles would not be filled before contracting during faster heart rates.
The function that relates APD to DI is known as the
restitution curve, and
it is an important property of cardiac tissue.
For further simulations visualizing the phase space see this applet.
The FHN model can be found in
FitzHugh R. (1961) Biophys J 1, 445-466.
or more information can be found, for example, in
Courtemanche M, Skaggs W, Winfree AT. (1990) Physica D 41, 173.